Marco Teórico

 Reseña Histórica

La regla de tres es una de las herramientas básicas de la aritmética elemental.

Esta regla se conoció en Occidente a través de los árabes. Varios autores árabes – entre ellos, al-Jwarizmi en su Álgebra – dan ejemplos que resuelven con este procedimiento, pero es al-Biruni quien dedica una obra completa a este tema.

Al-Biruni (973-1050) es uno de los científicos más notables de su época. Escribió un gran número de obras, se estima que más de 130, sobre muchos campos de conocimiento: matemáticas, astronomía, astrología, filosofía, cartografía y la India. Sus viajes a este país y su conocimiento del sánscrito le permietieron escribir acerca de su religión, su cultura, su geografía, su historia, su literatura y algunas cuestiones matemáticas.

Una de sus obras está dedicada a la regla de tres en la India. En esta obra señala que en la India se había generalizado este procedimiento tiempo atrás y que ellos conocían la regla de tres simple, directa, inversa y también la regla de tres compuesta.

No sabemos con seguridad desde qué momento se manejó sistemáticamente la regla de tres en la India. Uno de los documentos antiguos más interesantes que contienen esta regla es el Manuscrito Bakhshali. El nombre hace referencia a la ciudad, situada en la parte noroeste de la India, en cuyos alrededores se descubrió este texto en 1881. No se conoce el autor de la obra ni tampoco la fecha de redacción del original, sobre la que han existido hipótesis muy diversas. En la actualidad existe un cierto consenso sobre que podría ser una obra de principios de nuestra era.

El manuscrito, que en la actualidad se encuentra en Oxford, es un manual de reglas y ejemplos con sus soluciones. Contiene principalmente reglas y ejercicios de aritmética y álgebra, aunque tiene también problemas de mediciones.

¿Qué es una regla de tres simple?

La regla de tres simple es una operación que nos ayuda a resolver rápidamente problemas de proporcionalidad, tanto directa como inversa.

Para hacer una regla de tres simple necesitamos tres datos: dos magnitudes proporcionales entre sí, y una tercera magnitud. A partir de estos averiguaremosel cuarto término de la proporcionalidad.

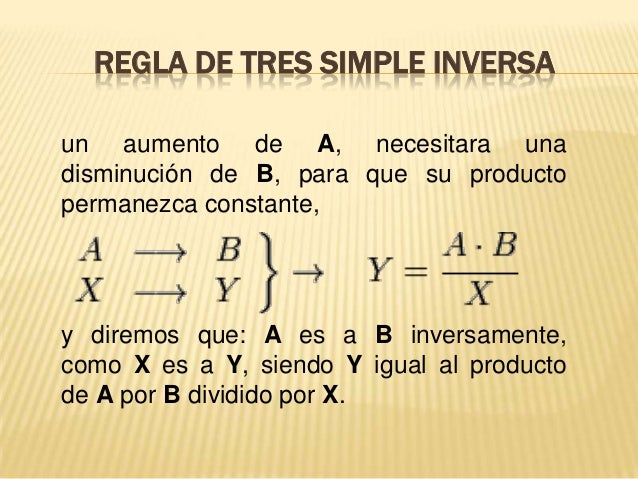
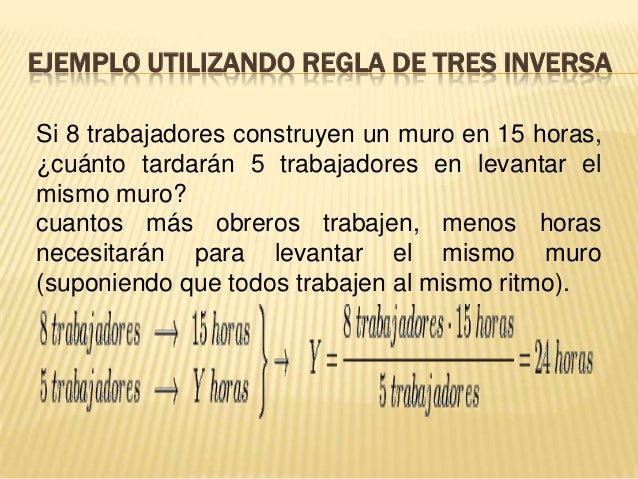
¿Qué es una regla de tres simple inversa?

Consiste en que dadas cantidades correspondientes a magnitudes inversamente proporcionales, callcular la cantidad de una de estas magnitudes correspondiente a una cantidad dada de la otra magnitud.
La regla de tres inversa la aplicaremos cuando entre las magnitudes se establecen las relaciones: a más menos.